在了解本章内容之前,请确定你至少已了解这一章的内容 线性变换-从向量到矩阵
行列式是什么
在回答这个问题之前,我们需要先了解以下内容⬇️
线性变换对区域面积的影响
如果在坐标系中划定一个区域
 坐标系在进行线性变换的过程中会,这个区域会发生形变,面积也有可能发生变化,这个面积的改变倍率是c,接下来我们所探究的内容就和c有关
坐标系在进行线性变换的过程中会,这个区域会发生形变,面积也有可能发生变化,这个面积的改变倍率是c,接下来我们所探究的内容就和c有关
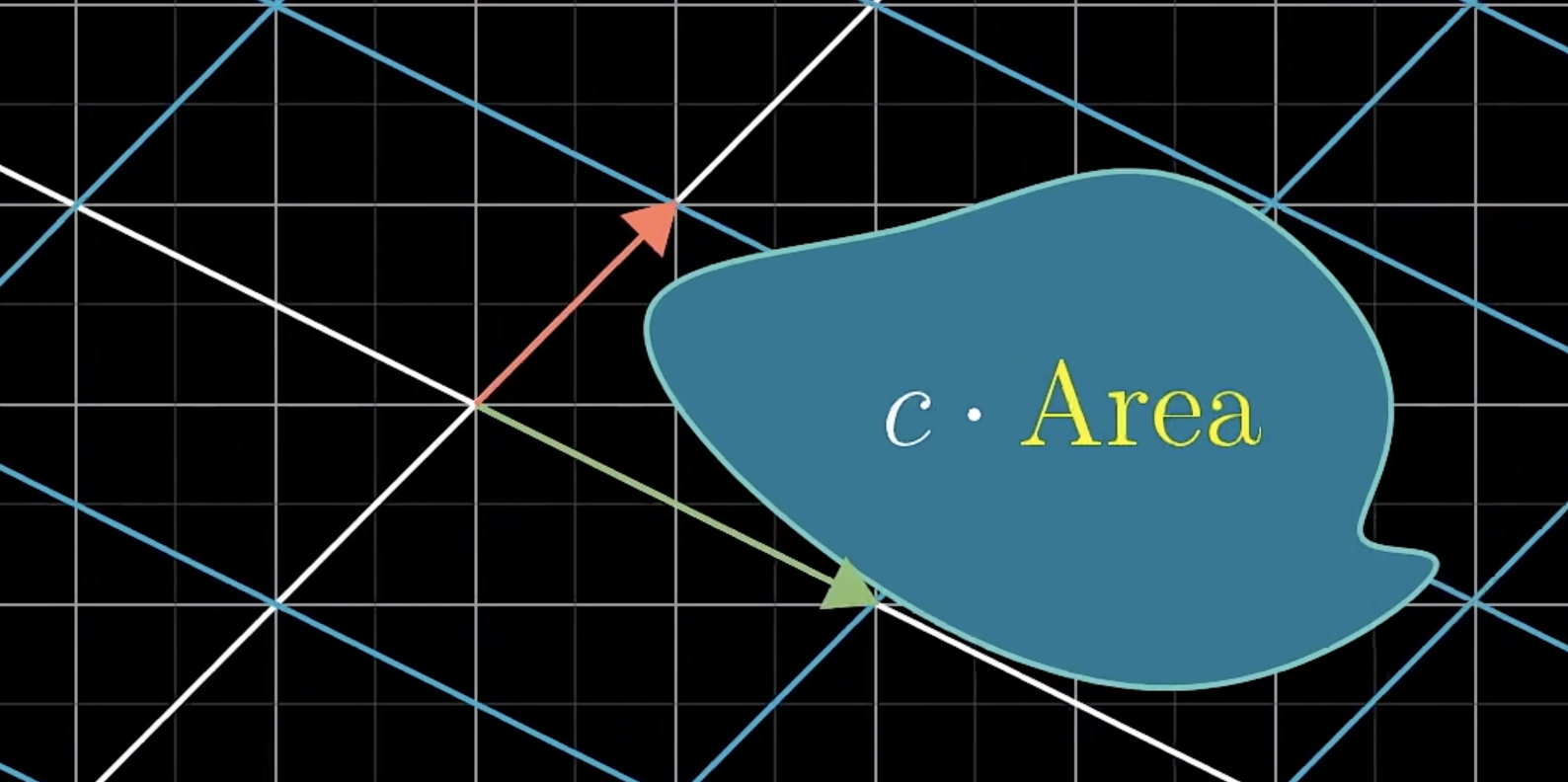 现在我们从简单的开始,探究由i,j向量围成的平行四边形面积
现在我们从简单的开始,探究由i,j向量围成的平行四边形面积
 !
我们进行如下变换:
!
我们进行如下变换:
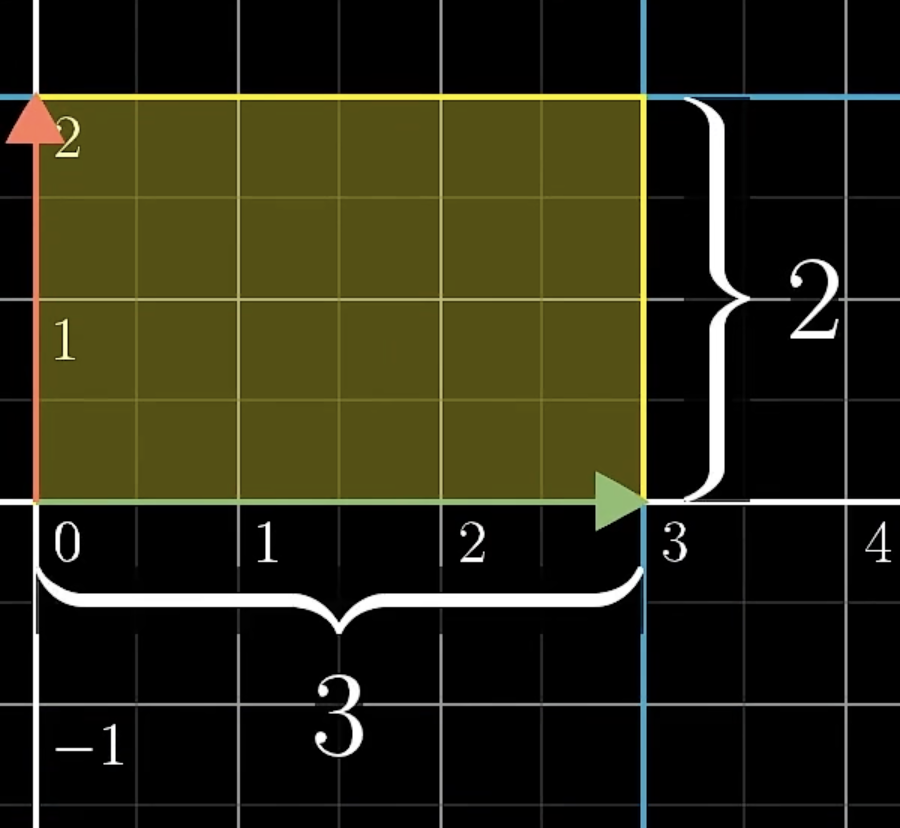 你可以由图像轻松的看出来它的面积是6,原先的面积为1也就是说 倍率
或者进行如下的变换:
你可以由图像轻松的看出来它的面积是6,原先的面积为1也就是说 倍率
或者进行如下的变换:
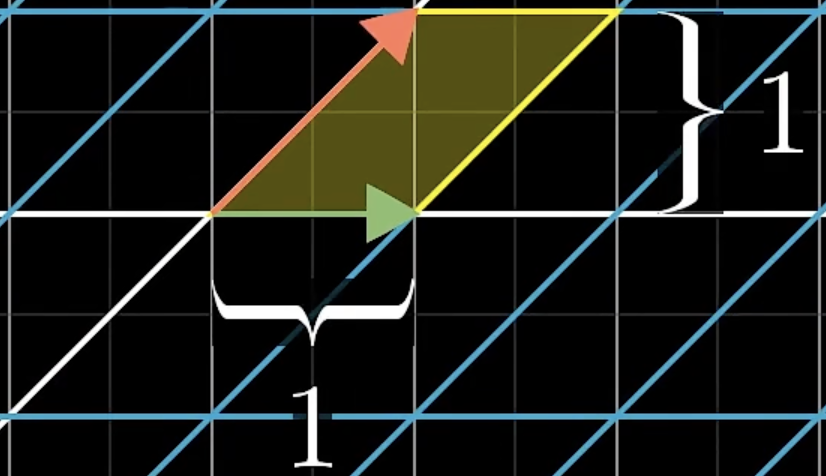 你可以由图像轻松的看出来它的面积是1,原先的面积为1也就是说 **倍率
你可以由图像轻松的看出来它的面积是1,原先的面积为1也就是说 **倍率
也就是说,在知道变换矩阵的条件下,你可以算出变换前后的单位面积改变倍数c 这个理论在线性变化下,不论讨论的图形是否规则均成立。
在了解了上述过程后,我们可以对行列式进行简单定义:
行列式是什么
现在我们可以对其进行定义了:
几何上,行列式是坐标系发生线性变换后单位图形相对于变换前的单位图形的面积改变的倍数
简单来说就是上面所说的,我们用数学公式表示如下:
解释:一个变换的行列式计算得c,说明坐标系发生线性变换后单位图形相对于变换前的单位图形的面积改变了c倍
另外说明:行列式的计算有可能是负数,并且这确实是正确的,无需在意,我个人对其的理解是: 一个x-y坐标系我们往往只观测其正面所以面积为正,当我们观测其背面的时候其面积为负。当线性变换得到一个负数时也想当于将坐标系翻转,改变了我们的观测方向,同样的,定义坐标系的单位向量和二者的方向关系也发生了反转(原先 j 在 i 的逆时针方向,如果变换后 j 在 i 的顺时针方向,我们也认为发生了坐标系发生翻转)。
上述解释需要等待我们了解行列式的计算,向量的叉乘以及其方向、大小的判定才能够了解。
行列式的计算
在上述的二维平面中,读者可以直观地从几何上推导出来其计算方式为对角相乘再相减:
如果在三维空间中,或许我们还可以勉强想象并模拟其行列式计算的几何意义,但是这是困难的: 我们可以想象空间中由,, 所围城的平行六面体的体积在空间发生线性变换后发生改变
在了解其原理后,记下计算公式就比较必要
你可以观察公式,形象化的记忆它
什么?你问我为什么不向上推导更高维度的行列式?
哥们洗洗睡吧,考试不考的